| |
|

|
|
|
|
| |
|

|
| |
 |
Code Conversion
|
|
|
Converting from one code form to another code form is called code conversion, like converting from binary to decimal or converting from hexadecimal to decimal. |
| |
|

|
| |
 |
Binary-To-Decimal Conversion
|
|
|
Any binary number can be converted to its decimal equivalent simply by summing together the weights of the various positions in the binary number which contain a 1. |
| |
|

|
|
|
|
Binary
|
Decimal
|
|
110112
|
|
|
24+23+01+21+20
|
=16+8+0+2+1
|
|
Result
|
2710
|
|
| |
|

|
|
|
and |
| |
|

|
|
|
|
Binary
|
Decimal
|
|
101101012
|
|
|
27+06+25+24+03+22+01+20
|
=128+0+32+16+0+4+0+1
|
|
Result
|
18110
|
|
| |
|

|
|
|
You should have noticed that the method is to find the weights (i.e., powers of 2) for each bit position that contains a 1, and then to add them up. |
| |
|

|
| |
 |
Decimal-To-Binary Conversion
|
| |
|

|
|
|
There are 2 methods: |
| |
|

|
|
|
- Reverse of Binary-To-Decimal Method
- Repeat Division
|
| |
|

|
| |
 |
Reverse of Binary-To-Decimal Method
|
| |
|

|
|
|
|
Decimal
|
Binary
|
|
4510
|
=32 + 0 + 8 + 4 +0 + 1
|
|
|
=25+0+23+22+0+20
|
|
Result
|
=1011012
|
|
| |
|

|
| |
|

|
| |
 |
Repeat Division-Convert decimal to binary
|
|
|
This method uses repeated division by 2. |
| |
|

|
|
|
Convert 2510 to binary |
| |
|

|
|
|
|
Division
|
Remainder
|
Binary
|
|
25/2
|
= 12+ remainder of 1
|
1 (Least Significant Bit)
|
|
12/2
|
= 6 + remainder of 0
|
0
|
|
6/2
|
= 3 + remainder of 0
|
0
|
|
3/2
|
= 1 + remainder of 1
|
1
|
|
1/2
|
= 0 + remainder of 1
|
1 (Most Significant Bit)
|
|
Result
|
2510
|
= 110012
|
|
| |
|

|
|
|
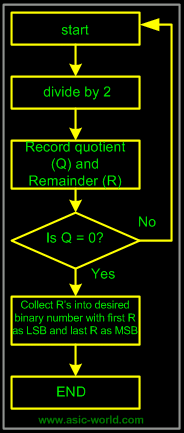
The Flow chart for repeated-division method is as follows: |
| |
|

|
|
|
 |
| |
|

|
|
|
|
| |
|

|
| |
 |
Binary-To-Octal / Octal-To-Binary Conversion
|
| |
|

|
|
|
|
Octal Digit
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
Binary Equivalent
|
000
|
001
|
010
|
011
|
100
|
101
|
110
|
111
|
|
| |
|

|
|
|
Each Octal digit is represented by three binary digits. |
| |
|

|
|
|
Example: |
|
|
100 111 0102 = (100) (111) (010)2 = 4 7 28 |
| |
|

|
| |
 |
Repeat Division-Convert decimal to octal
|
| |
|

|
|
|
This method uses repeated division by 8. |
| |
|

|
|
|
Example: Convert 17710 to octal and binary |
| |
|

|
|
|
|
Division
|
Result
|
Binary
|
|
177/8
|
= 22+ remainder of 1
|
1 (Least Significant Bit)
|
|
22/ 8
|
= 2 + remainder of 6
|
6
|
|
2 / 8
|
= 0 + remainder of 2
|
2 (Most Significant Bit)
|
|
Result
|
17710
|
= 2618
|
|
Binary
|
|
= 0101100012
|
|
| |
|

|
| |
 |
Hexadecimal to Decimal/Decimal to Hexadecimal Conversion
|
| |
|

|
|
|
Example: |
|
|
2AF16 = 2 x (162) + 10 x (161) + 15 x (160) = 68710 |
| |
|

|
| |
 |
Repeat Division- Convert decimal to hexadecimal
|
|
|
This method uses repeated division by 16. |
| |
|

|
|
|
Example: convert 37810 to hexadecimal and binary: |
| |
|

|
|
|
|
Division
|
Result
|
Hexadecimal
|
|
378/16
|
= 23+ remainder of 10
|
A (Least Significant Bit)23
|
|
23/16
|
= 1 + remainder of 7
|
7
|
|
1/16
|
= 0 + remainder of 1
|
1 (Most Significant Bit)
|
|
Result
|
37810
|
= 17A16
|
|
Binary
|
|
= 0001 0111 10102
|
|
| |
|

|
| |
 |
Binary-To-Hexadecimal /Hexadecimal-To-Binary Conversion
|
| |
|

|
|
|
|
Hexadecimal Digit
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
Binary Equivalent
|
0000
|
0001
|
0010
|
0011
|
0100
|
0101
|
0110
|
0111
|
|
| |
|

|
|
|
|
Hexadecimal Digit
|
8
|
9
|
A
|
B
|
C
|
D
|
E
|
F
|
|
Binary Equivalent
|
1000
|
1001
|
1010
|
1011
|
1100
|
1101
|
1110
|
1111
|
|
| |
|

|
|
|
Each Hexadecimal digit is represented by four bits of binary digit. |
| |
|

|
|
|
Example: |
| |
|

|
|
|
1011 0010 11112 = (1011) (0010) (1111)2 = B 2 F16 |
| |
|

|
| |
 |
Octal-To-Hexadecimal Hexadecimal-To-Octal Conversion
|
| |
|

|
|
|
- Convert Octal (Hexadecimal) to Binary first.
- Regroup the binary number by three bits per group starting from LSB if Octal is required.
- Regroup the binary number by four bits per group starting from LSB if Hexadecimal is required.
|
| |
|

|
|
|
Example: |
| |
|

|
|
|
Convert 5A816 to Octal. |
| |
|

|
|
|
|
Hexadecimal
|
Binary/Octal
|
|
5A816
|
= 0101 1010 1000 (Binary)
|
|
|
= 010 110 101 000 (Binary)
|
|
Result
|
= 2 6 5 0 (Octal)
|
|
| |
|

|
| |
|

|
| |
|

|
|
|
|
| |
|

|